Mark's wife works a pharmaceutical company as a research scientist.
Mark's wife works _____ a pharmaceutical company as a research scientist.
Choose the mistake:
Mark used to work like a teacher before he pursued a career as a software engineer.
Choose the mistake:
Mark used to work like a teacher before he pursued a career as a software engineer.
Choose the mistake:
The news in the radio alerted everyone about the upcoming storm.
Choose the mistake:
The news in the radio alerted everyone about the upcoming storm.
The school cafeteria provides students nutritious meals to support their learning.
The school cafeteria provides students _____ nutritious meals to support their learning.
The hotel provides complimentary breakfast guests staying overnight.
The hotel provides complimentary breakfast _____ guests staying overnight.
The fall in retail sales is directly connected the decline in employment.
The fall in retail sales is directly connected _____ the decline in employment.
Choose the mistake:
She never expected to get involved in someone like him, but their shared values and sense of humor ?
Choose the mistake:
She never expected to get involved in someone like him, but their shared values and sense of humor brought them together.
Choose the phrase that is closest in meaning to the underlined part:
Sarah decided to get involved in the neighborhood ?
Choose the phrase that is closest in meaning to the underlined part:
Sarah decided to get involved in the neighborhood cleanup effort to help improve the environment.
The document should make no reference sensitive financial data.
The document should make no reference _____ sensitive financial data.
The museum downtown is a popular place interest for visitors.
The museum downtown is a popular place _____ interest for visitors.
Choose the mistake:
As a parent, I want to invest to my child's future by providing them with a quality education.
Choose the mistake:
As a parent, I want to invest to my child's future by providing them with a quality education.
In the summer the beach is crowded visitors.
In the summer the beach is crowded _____ visitors.
He's willing to others' perspectives before making a decision.
He's willing _____ to others' perspectives before making a decision.
The teacher called each student name to distribute their test papers.
The teacher called each student _____ name to distribute their test papers.
The amount of protein you need is directly related your lifestyle.
The amount of protein you need is directly related _____ your lifestyle.
Choose the word that is closest in meaning to the underlined part:
They finally had the chance to meet face to face aft?
Choose the word that is closest in meaning to the underlined part:
They finally had the chance to meet face to face after months of communicating online.
Choose the mistake:
He's interested on learning to play the guitar and has signed up for beginner lessons at the local ?
Choose the mistake:
He's interested on learning to play the guitar and has signed up for beginner lessons at the local music school.
Choose the phrase that is closest in meaning to the underlined part:
Local police say that youth crime is on the rise i?
Choose the phrase that is closest in meaning to the underlined part:
Local police say that youth crime is on the rise in the area.
Glue won’t adhere any surface that’s wet.
Glue won’t adhere _____ any surface that’s wet.
Their children lived together perfect harmony.
Their children lived together _____ perfect harmony.
Nung nóng hỗn hợp X gồm metan, etilen, propin, vinyl axetilen và a mol H2 có Ni xúc tác (chỉ xảy ra phản ứng cộng H2), t?
Nung nóng hỗn hợp X gồm metan, etilen, propin, vinyl axetilen và a mol H2 có Ni xúc tác (chỉ xảy ra phản ứng cộng H2), thu được 0,4 mol hỗn hợp Y (gồm các hiđrocacbon) có tỉ khối so với H2 là 18. Biết 0,1 mol Y phản ứng tối đa với 0,05 mol Br2 trong dung dịch. Giá trị của a là
Dẫn từ từ đến dư khí CO2 vào dung dịch chứa 0,2 mol Ba(OH)2. Sự phụ thuộc của số mol kết tủa (a mol) vào số mol khí CO2 ?
Dẫn từ từ đến dư khí CO2 vào dung dịch chứa 0,2 mol Ba(OH)2. Sự phụ thuộc của số mol kết tủa (a mol) vào số mol khí CO2 tham gia phản ứng (b mol) được biểu diễn như đồ thị sau:
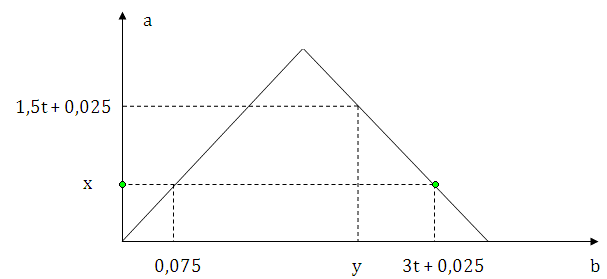
Tỉ lệ y : x là
Hỗn hợp X chứa ba este thuần chức, mạch hở gồm một este đơn chức và hai este hai chức. Đun nóng 0,2 mol X với dung dịch ?
Hỗn hợp X chứa ba este thuần chức, mạch hở gồm một este đơn chức và hai este hai chức. Đun nóng 0,2 mol X với dung dịch NaOH vừa đủ, thu được 26,32 gam muối duy nhất và hỗn hợp Y gồm ba ancol no, trong đó có hai ancol hơn kém nhau một nguyên tử cacbon. Đốt cháy hoàn toàn Y cần dùng 0,545 mol O2, thu được 10,62 gam H2O. Phần trăm khối lượng của este hai chức có khối lượng phân tử lớn trong X là
Đun nóng m gam hỗn hợp E chứa triglixerit X và các axit béo tự do với 300 ml dung dịch KOH 1M (vừa đủ), thu được glixero?
Đun nóng m gam hỗn hợp E chứa triglixerit X và các axit béo tự do với 300 ml dung dịch KOH 1M (vừa đủ), thu được glixerol và hỗn hợp Y chứa các muối có công thức chung C17HyCOOK. Đốt cháy 0,14 mol E, thu được 3,69 mol CO2. Mặt khác, m gam E tác dụng vừa đủ với 0,25 mol Br2. Biết các phản ứng xảy ra hoàn toàn. Giá trị của m là
Cho sơ đồ phản ứng theo đúng tỉ lệ mol như sau:
(1) X + 2NaOH → 2X1 + X2
(2) X1 + HCl → X3 + NaCl
(3) X2 + 2AgNO3 + 3?
Cho sơ đồ phản ứng theo đúng tỉ lệ mol như sau:
(1) X + 2NaOH → 2X1 + X2
(2) X1 + HCl → X3 + NaCl
(3) X2 + 2AgNO3 + 3NH3 + H2O → X4 + 2NH4NO3 + 2Ag↓
Biết X mạch hở, có công thức phân tử là C6H8O5; X1 có hai nguyên tử cacbon trong phân tử. Cho các phát biểu sau:
(a) Đốt cháy 1,2 mol X1 cần vừa đủ 1,8 mol O2 (hiệu suất phản ứng 100%).
(b) X3 là hợp chất hữu cơ tạp chức.
(c) Phân tử khối của X1 là 82.
(d) Phân tử X4 có bảy nguyên tử hiđro.
(e) X2 là axetanđehit.
Số phát biểu đúng là
Hỗn hợp hơi X chứa butan, butylamin, isopropyl axetat. Đốt cháy hoàn toàn m gam (tương ứng với 0,15 mol) gồm valin và X ?
Hỗn hợp hơi X chứa butan, butylamin, isopropyl axetat. Đốt cháy hoàn toàn m gam (tương ứng với 0,15 mol) gồm valin và X cần dùng 0,9975 mol O2, thu được CO2, H2O và N2. Mặt khác, m gam hỗn hợp valin và X phản ứng vừa hết với 60 ml dung dịch NaOH 1M. Giá trị của m là
Cho 4,536 gam hỗn hợp chất rắn X gồm Mg, MgCO3 và Mg(NO3)2 (trong đó, nguyên tố oxi chiếm 28,57% về khối lượng hỗn hợp) ?
Cho 4,536 gam hỗn hợp chất rắn X gồm Mg, MgCO3 và Mg(NO3)2 (trong đó, nguyên tố oxi chiếm 28,57% về khối lượng hỗn hợp) vào dung dịch chứa 0,018 mol HNO3 và 0,246 mol KHSO4, khuấy đều cho các phản ứng xảy ra hoàn toàn, thu được dung dịch Y chỉ chứa các muối trung hòa có khối lượng 36,198 gam và hỗn hợp khí Z gồm N2O, N2, CO2 và H2 (trong đó số mol của N2O bằng số mol của CO2). Phần trăm về số mol của N2 trong Z là
Tiến hành thí nghiệm theo các bước sau:
– Bước 1: Cho 5 giọt dung dịch CuSO4 0,5% vào ống nghiệm sạch.
– Bước 2: Thêm 1 ?
Tiến hành thí nghiệm theo các bước sau:
– Bước 1: Cho 5 giọt dung dịch CuSO4 0,5% vào ống nghiệm sạch.
– Bước 2: Thêm 1 ml dung dịch NaOH 10% vào ống nghiệm, lắc đều; gạn phần dung dịch, giữ lại kết tủa.
– Bước 3: Thêm tiếp 2 ml dung dịch glucozơ 1% vào ống nghiệm, lắc đều.
Cho các phát biểu sau:
(a) Sau bước 2 thu được kết tủa màu đỏ.
(b) Nếu thay dung dịch NaOH ở bước 2 bằng dung dịch KOH thì hiện tượng ở bước 3 vẫn tương tự.
(c) Sau bước 3, kết tủa đã bị hòa tan, thu được dung dịch màu tím.
(d) Ở bước 3, nếu thay glucozơ bằng saccarozơ thì hiện tượng xảy ra vẫn tương tự.
(e) Thí nghiệm trên chứng minh glucozơ có tính chất của anđehit.
Số phát biểu đúng là
Tiến hành các thí nghiệm sau:
(a) Dẫn 2a mol CO2 vào dung dịch chứa a mol Ba(OH)2 và a mol NaOH.
(b) Cho dung dịch Ba(?
Tiến hành các thí nghiệm sau:
(a) Dẫn 2a mol CO2 vào dung dịch chứa a mol Ba(OH)2 và a mol NaOH.
(b) Cho dung dịch Ba(NO3)2 vào dung dịch NaHCO3.
(c) Cho hỗn hợp bột Cu và Fe2(SO4)3 (tỉ lệ mol 1:1) vào nước dư.
(d) Cho 5a mol Mg vào dung dịch chứa 2a mol FeCl3.
(e) Cho dung dịch AgNO3 vào dung dịch FeCl3.
Sau khi các phản ứng xảy ra hoàn toàn, số thí nghiệm thu được kết tủa là
Cho sơ đồ chuyển hóa: A$\text{NaOH}\xrightarrow{\text{+X}}\text{Z}\xrightarrow{\text{+Y}}\text{NaOH}\xrightarrow{\text{+?
Cho sơ đồ chuyển hóa:
$\text{NaOH}\xrightarrow{\text{+X}}\text{Z}\xrightarrow{\text{+Y}}\text{NaOH}\xrightarrow{\text{+X}}\text{E}\xrightarrow{\text{+Y}}\text{CaC}{{\text{O}}_{\text{3}}}.$
Biết: X, Y, Z, E là các hợp chất khác nhau và khác CaCO3; mỗi mũi tên ứng với một phương trình hóa học của phản ứng giữa hai chất tương ứng. Các chất X, Y thỏa mãn sơ đồ trên lần lượt là
Cho 6,2 gam hợp chất hữu cơ X có công thức phân tử là C3H12O3N2 tác dụng vừa đủ với 100 ml dung dịch NaOH 1M, thu được m?
Cho 6,2 gam hợp chất hữu cơ X có công thức phân tử là C3H12O3N2 tác dụng vừa đủ với 100 ml dung dịch NaOH 1M, thu được một chất hữu cơ ở thể khí có thể tích là V lít (ở đktc) và dung dịch Z chỉ chứa các chất vô cơ, cô cạn dung dịch Z thu được m gam chất rắn khan. Giá trị của m và V lần lượt là:
Cho các phát biểu sau:
(a) Đun chất béo với dung dịch Ca(OH)2 trong thùng kín ở nhiệt độ cao, thu được xà phòng.
(b) Tú?
Cho các phát biểu sau:
(a) Đun chất béo với dung dịch Ca(OH)2 trong thùng kín ở nhiệt độ cao, thu được xà phòng.
(b) Túi nilon làm từ nhựa polietilen rất khó bị phân hủy, gây ô nhiễm cho môi trường.
(c) Đipeptit Glu-Lys tác dụng với dung dịch HCl theo tỉ lệ mol 1 : 2.
(d) Dung dịch alanin tạo kết tủa trắng với nước brom.
(e) Tơ tằm kém bền trong môi trường axit và môi trường kiềm.
Số phát biểu đúng là
Cho 11,6 gam Fe vào 100 ml dung dịch CuSO4 1M. Sau khi phản ứng xảy ra hoàn toàn, thu được m gam hỗn hợp kim loại. Giá t?
Cho 11,6 gam Fe vào 100 ml dung dịch CuSO4 1M. Sau khi phản ứng xảy ra hoàn toàn, thu được m gam hỗn hợp kim loại. Giá trị của m là
Thủy phân hoàn toàn hỗn hợp metyl axetat và metyl acrylat trong dung dịch NaOH, thu được sản phẩm gồm
Thủy phân hoàn toàn hỗn hợp metyl axetat và metyl acrylat trong dung dịch NaOH, thu được sản phẩm gồm
Chất X được dùng làm thuốc tăng lực cho người già, trẻ nhỏ và người ốm. Trong công nghiệp, X dùng làm nguyên liệu để điề?
Chất X được dùng làm thuốc tăng lực cho người già, trẻ nhỏ và người ốm. Trong công nghiệp, X dùng làm nguyên liệu để điều chế chất Y. Y được dùng để sản xuất xăng E5. Phát biểu nào sau đây sai?
Phát biểu nào sau đây sai?
Phát biểu nào sau đây sai?
Thực hiện phản ứng tráng gương 36 gam dung dịch fructozơ 10% với lượng dung dịch AgNO3 trong NH3, nếu hiệu suất phản ứng?
Thực hiện phản ứng tráng gương 36 gam dung dịch fructozơ 10% với lượng dung dịch AgNO3 trong NH3, nếu hiệu suất phản ứng 40% thì khối lượng bạc kim loại thu được là
X là kim loại phản ứng được với dung dịch H2SO4 loãng, Y là kim loại tác dụng được với dung dịch Fe(NO3)3. Hai kim loại ?
X là kim loại phản ứng được với dung dịch H2SO4 loãng, Y là kim loại tác dụng được với dung dịch Fe(NO3)3. Hai kim loại X, Y lần lượt là
Đun nóng 14,6 gam Gly-Ala với lượng dư dung dịch NaOH. Sau khi phản ứng xảy ra hoàn toàn, thu được dung dịch chứa m gam ?
Đun nóng 14,6 gam Gly-Ala với lượng dư dung dịch NaOH. Sau khi phản ứng xảy ra hoàn toàn, thu được dung dịch chứa m gam muối. Giá trị của m là
Đốt cháy hoàn toàn m gam glyxin trong O2 thu được N2, H2O và 2,24 lít CO2 (ở đktc). Giá trị của m là
Đốt cháy hoàn toàn m gam glyxin trong O2 thu được N2, H2O và 2,24 lít CO2 (ở đktc). Giá trị của m là
[OPPOSITE] - You can leave the butter out of the recipe if you're on a low-fat diet.
[OPPOSITE] - You can leave the butter out of the recipe if you're on a low-fat diet.
The director leaned many things to decide for Jenny to resign.
The director leaned _____ many things to decide for Jenny to resign.
[MISTAKE] - Eating a large amount of fast food could lead on excess calories and increase the risk of obesity.
[MISTAKE] - Eating a large amount of fast food could lead on excess calories and increase the risk of obesity.
[CLOSEST] - In the middle of the yesterday's meeting, Mr. John suddenly laid into four employees for no apparent reason.
[CLOSEST] - In the middle of the yesterday's meeting, Mr. John suddenly laid into four employees for no apparent reason.
[OPPOSITE] - The manager laid down the regulations for all new employees in the department.
[OPPOSITE] - The manager laid down the regulations for all new employees in the department.
Mary tried to laugh their remarks, but I could see she was hurt.
Mary tried to laugh _____ their remarks, but I could see she was hurt.
[OPPOSITE] - The team knocked out their opponents in the final match to win the championship.
[OPPOSITE] - The team knocked out their opponents in the final match to win the championship.
My mom prepared dinner and brought it to my workplace as I had a ton of deadlines and I wouldn’t knock until 9 p.m.
My mom prepared dinner and brought it to my workplace as I had a ton of deadlines and I wouldn’t knock _____ until 9 p.m.
[CLOSEST] - The strong earthquake knocked down the buildings and caused widespread damage.
[CLOSEST] - The strong earthquake knocked down the buildings and caused widespread damage.
Students mustn't keep the grass because the school strictly prohibits stepping on as well as damaging it.
Students mustn't keep _____ the grass because the school strictly prohibits stepping on as well as damaging it.
Cho biết tình hình thu hoạch lúa vụ mùa năm $2022$ của ba hợp tác xã ở một địa phương như sau:Khi đó:
Cho biết tình hình thu hoạch lúa vụ mùa năm $2022$ của ba hợp tác xã ở một địa phương như sau:
Khi đó:
“Công việc kinh doanh thành công giúp ai ấy kiếm được rất nhiều tiền.”
=> His successful business helps him create a?
“Công việc kinh doanh thành công giúp ai ấy kiếm được rất nhiều tiền.”
=> His successful business helps him create a fortune.
“Cô ấy quyết định đi leo núi để thoát khỏi nhịp sống bận rộn.”
=> She decides to climb the mountain in order to esca?
“Cô ấy quyết định đi leo núi để thoát khỏi nhịp sống bận rộn.”
=> She decides to climb the mountain in order to escape the hectic pace of life.
“Sau nhiều năm làm việc trong ngành công nghiệp, cô ấy nắm rõ quy định như lòng bàn tay.”
=> After years of working ?
“Sau nhiều năm làm việc trong ngành công nghiệp, cô ấy nắm rõ quy định như lòng bàn tay.”
=> After years of working in the industry, she knows the regulations like the back of her hand.
“Đầu tư vào các sản phẩm thân thiện với môi trường và công nghệ rất cần thiết để giảm thiểu ô nhiễm môi trường.”
=> ?
“Đầu tư vào các sản phẩm thân thiện với môi trường và công nghệ rất cần thiết để giảm thiểu ô nhiễm môi trường.”
=> Investing in environmental-friendly products and technologies is essential for reducing pollution.
“Sử dụng các nguồn năng lượng tái tạo như năng lượng mặt trời hoặc năng lượng gió là cách hiệu quả để giảm thiểu lượng k?
“Sử dụng các nguồn năng lượng tái tạo như năng lượng mặt trời hoặc năng lượng gió là cách hiệu quả để giảm thiểu lượng khí thải carbon.”
=> Using renewable energy sources like solar or wind power is an effective way to reduce carbon footprint.
“Tần suất các hiện tượng thời tiết cực đoan đang tăng lên do biến đổi khí hậu.”
=> The frequency of extreme weather ?
“Tần suất các hiện tượng thời tiết cực đoan đang tăng lên do biến đổi khí hậu.”
=> The frequency of extreme weather events is increasing due to climate alteration.
Chất X làm cho nước biển có vị mặn, được sử dụng phổ biến như là gia vị và chất bảo quản thực phẩm. Công thức của X là
Chất X làm cho nước biển có vị mặn, được sử dụng phổ biến như là gia vị và chất bảo quản thực phẩm. Công thức của X là
Các este thường có mùi thơm đặc trưng, etyl propionat có mùi dứa. Công thức cấu tạo thu gọn của etyl propionat là
Các este thường có mùi thơm đặc trưng, etyl propionat có mùi dứa. Công thức cấu tạo thu gọn của etyl propionat là
Muối mono natri của amino axit nào sau đây được dùng làm bột ngọt (mì chính)?
Muối mono natri của amino axit nào sau đây được dùng làm bột ngọt (mì chính)?
Ở điều kiện thích hợp, este nào sau đây có phản ứng tráng gương?
Ở điều kiện thích hợp, este nào sau đây có phản ứng tráng gương?
Thí nghiệm Cu tác dụng với axit HNO3 đặc, giải phóng khí NO2 rất độc. Để loại bỏ NO2, sau khi cho Cu vào ống nghiệm, ngư?
Thí nghiệm Cu tác dụng với axit HNO3 đặc, giải phóng khí NO2 rất độc. Để loại bỏ NO2, sau khi cho Cu vào ống nghiệm, người ta nút ống nghiệm bằng bông tẩm dung dịch chất X. Công thức của X là
“Bảo vệ môi trường sống tự nhiên là vô cùng quan trọng để bảo vệ đa dạng sinh học và các loài gặp nguy hiểm.”
=> Con?
“Bảo vệ môi trường sống tự nhiên là vô cùng quan trọng để bảo vệ đa dạng sinh học và các loài gặp nguy hiểm.”
=> Conserving natural habitats is absolutely vital for protecting biodiversity and dangerous species.
“ Các kiểu thời tiết như lốc xoáy và bão tuyết có thể làm gián đoạn hệ thống giao thông và gây thiệt hại cho cơ sở hạ tầ?
“ Các kiểu thời tiết như lốc xoáy và bão tuyết có thể làm gián đoạn hệ thống giao thông và gây thiệt hại cho cơ sở hạ tầng.”
=> Weather patterns like tornadoes and blizzards can disrupt transportation systems and cause damage to infrastructure.
“Ô nhiễm từ các nhà máy và ô tô gây hại cho môi trường và góp phần gây biến đổi khí hậu.”
=> Pollution from factorie?
“Ô nhiễm từ các nhà máy và ô tô gây hại cho môi trường và góp phần gây biến đổi khí hậu.”
=> Pollution from factories and cars is harmful to the environment and contributes to climate change.
“Tái chế giấy, nhựa và thủy tinh giúp giảm thiểu rác thải và bảo vệ môi trường.”
=> Reusing paper, plastic, and glas?
“Tái chế giấy, nhựa và thủy tinh giúp giảm thiểu rác thải và bảo vệ môi trường.”
=> Reusing paper, plastic, and glass helps reduce waste and protect the environment.
Hàm lượng Natri (đơn vị miligam, ${1 {mg}=0,001 {~g}}$) trong ${100 {~g}}$ một số loại ngũ cốc được cho như sau:Khi đó:
Hàm lượng Natri (đơn vị miligam, ${1 {mg}=0,001 {~g}}$) trong ${100 {~g}}$ một số loại ngũ cốc được cho như sau:

Khi đó:
“Đối mặt với nhiều lời mời làm việc, cô ấy phải cẩn thận xem xét trước khi đưa ra quyết định.”
=> Facing multiple jo?
“Đối mặt với nhiều lời mời làm việc, cô ấy phải cẩn thận xem xét trước khi đưa ra quyết định.”
=> Facing multiple job offers, she must carefully consider before _____.
“Sau vài vòng thảo luận, chúng tôi có thể đạt được sự thỏa thuận về dự án.”
=> After several rounds of discussions, ?
“Sau vài vòng thảo luận, chúng tôi có thể đạt được sự thỏa thuận về dự án.”
=> After several rounds of discussions, we are able to ____ an agreement on the project.
“Rất quan trọng cho các nhà cung cấp dịch vụ chăm sóc sức khỏe để tuân thủ các chất lượng vệ sinh nghiêm ngặt.”
=> I?
“Rất quan trọng cho các nhà cung cấp dịch vụ chăm sóc sức khỏe để tuân thủ các chất lượng vệ sinh nghiêm ngặt.”
=> It's crucial for healthcare providers to ____ strict hygiene standards.
“Quốc hội đã thông qua những bộ luật mới nhằm mục tiêu cải thiện các biện pháp bảo vệ môi trường.”
=> The parliament?
“Quốc hội đã thông qua những bộ luật mới nhằm mục tiêu cải thiện các biện pháp bảo vệ môi trường.”
=> The parliament has ____ new laws aimed at improving environmental protection measures.
“Bất chấp những khuyết điểm của anh, cô ấy vẫn đánh giá cao anh vì trái tim nhân hậu và sự sẵn sàng giúp đỡ người khác.”?
“Bất chấp những khuyết điểm của anh, cô ấy vẫn đánh giá cao anh vì trái tim nhân hậu và sự sẵn sàng giúp đỡ người khác.”
=> Despite his flaws, she still _____ him because of his kind heart and willingness to help others.
“Khung cảnh ngoạn mục của ngọn núi đã gây ấn tượng lâu dài cho anh ấy.”
=> The breathtaking scenery of the mountains ma?
“Khung cảnh ngoạn mục của ngọn núi đã gây ấn tượng lâu dài cho anh ấy.”
=> The breathtaking scenery of the mountains made a ____ impression on him.
“Toàn đội ăn mừng chiến thắng đầy thuyết phục với tiếng reo hò và đập tay.”
=> The team celebrated their victory wi?
“Toàn đội ăn mừng chiến thắng đầy thuyết phục với tiếng reo hò và đập tay.”
=> The team celebrated their _____ victory with cheers and high-fives.
“Khán giả đứng dậy vỗ tay khi đội bóng bước vào sân.”
=> The stood and clapped as the football teams went on to the?
“Khán giả đứng dậy vỗ tay khi đội bóng bước vào sân.”
=> The ____ stood and clapped as the football teams went on to the pitch.
“Khi họ đề nghị thăng chức cho cô với múc lương cao hơn, cô ấy chớp lấy cơ hội mà không do dự.”
=> When they offer h?
“Khi họ đề nghị thăng chức cho cô với múc lương cao hơn, cô ấy chớp lấy cơ hội mà không do dự.”
=> When they offer her a promotion with a higher salary, she _____ at the chance without hesitation.
“Cuối cùng anh ấy cũng thành thạo cách sử dụng đũa và có thể tận hưởng món sushi mà không làm rơi nó liên tục.”
=> E?
“Cuối cùng anh ấy cũng thành thạo cách sử dụng đũa và có thể tận hưởng món sushi mà không làm rơi nó liên tục.”
=> Eventually, he ____ using chopsticks and could enjoy his sushi without dropping it all the time.
“Trong chuyến đi thám hiểm, chúng tôi phải đối mặt với điều kiện thời tiết khắc nghiệt, bao gồm tuyết rơi dày đặc và nhi?
“Trong chuyến đi thám hiểm, chúng tôi phải đối mặt với điều kiện thời tiết khắc nghiệt, bao gồm tuyết rơi dày đặc và nhiệt độ đóng băng.”
=> During our expedition, we faced severe weather circumstances, including heavy snowfall and freezing temperatures.
“Thác nước nằm ở một ngôi làng hơi hẻo lánh ít người biết đến.”
=> The waterfall is located in a village that is a litt?
“Thác nước nằm ở một ngôi làng hơi hẻo lánh ít người biết đến.”
=> The waterfall is located in a village that is a little bit off the beaten track.
“Bác sĩ cho anh ấy những loại thuốc mạnh hơn với hy vọng hão huyền rằng anh ấy có thể hồi phục.”
=> The doctors gave hi?
“Bác sĩ cho anh ấy những loại thuốc mạnh hơn với hy vọng hão huyền rằng anh ấy có thể hồi phục.”
=> The doctors gave him more powerful drugs in the vain hope that he might recover.
“Công ty tôi lên kế hoạch cùng nhau đi thăm quan xung quanh các địa danh và địa điểm nổi tiếng của thành phố.”
=> My?
“Công ty tôi lên kế hoạch cùng nhau đi thăm quan xung quanh các địa danh và địa điểm nổi tiếng của thành phố.”
=> My company plans to go for sightseeing around the city's famous landmarks and attractions.
“Sau chuyến đi đầy gian khổ, chúng tôi cuối cùng cũng đến được ngôi làng hẻo lánh ẩn mình trong thung lũng.”
=> Afte?
“Sau chuyến đi đầy gian khổ, chúng tôi cuối cùng cũng đến được ngôi làng hẻo lánh ẩn mình trong thung lũng.”
=> After an arduous journey, we finally reached the remote village nestled in the valley.
“Tôi đặt chuyến bay với một hãng hàng không giá rẻ để tiết kiệm tiền trong chuyến đi châu Âu.”
=> I booked my flight?
“Tôi đặt chuyến bay với một hãng hàng không giá rẻ để tiết kiệm tiền trong chuyến đi châu Âu.”
=> I booked my flight with a low-cut airline to save money on my trip to Europe.
“Bố tôi muốn dành mùa hè này để đi khám phá những địa điểm thu hút khách du lịch nổi tiếng vì ông ấy muốn đi du lịch đâu?
“Bố tôi muốn dành mùa hè này để đi khám phá những địa điểm thu hút khách du lịch nổi tiếng vì ông ấy muốn đi du lịch đâu đó.
=> My dad wants to spend this summer discovering more famous tourist attractions because he gets itchy feet.
“ Cô gái không thể kìm được sự phấn chấn khi mở gói hàng chờ đợi đã lâu.”
=> The girl is unable to contain her excit?
“ Cô gái không thể kìm được sự phấn chấn khi mở gói hàng chờ đợi đã lâu.”
=> The girl is unable to contain her excitement as she opens the long-awaited package.
“Thế hệ tương lai nên trân trọng và bảo tồn di sản văn hóa của đất nước.”
=> The future generation should cherish a?
“Thế hệ tương lai nên trân trọng và bảo tồn di sản văn hóa của đất nước.”
=> The future generation should cherish and preserve the country’s cultural inherit.
“Hàng triệu người địa phương và du khách tham gia lễ hội cái được tổ chức mỗi năm một lần.”
=> Hundreds of local peo?
“Hàng triệu người địa phương và du khách tham gia lễ hội cái được tổ chức mỗi năm một lần.”
=> Hundreds of local people and tourists join on the festival which is celebrated once a year.
Cho mẫu số liệu sau: $21\,\,\,35\,\,\,17\,\,\,43\,\,\,8\,\,\,59\,\,\,72\,\,\,74\,\,\,55$. Khi đó:
Cho mẫu số liệu sau: $21\,\,\,35\,\,\,17\,\,\,43\,\,\,8\,\,\,59\,\,\,72\,\,\,74\,\,\,55$. Khi đó:
“Tham gia lễ hội thu hoạch đã trở thành truyền thống lâu đời của gia đình tôi.”
=> Attending the annual harvest fest?
“Tham gia lễ hội thu hoạch đã trở thành truyền thống lâu đời của gia đình tôi.”
=> Attending the annual harvest festival has become a long-standing tradition in our family.
“Mỗi mùa hè, thị trấn nhỏ ven biển lại tổ chức màn bắn pháo hoa ngoạn mục.”
=> Every summer, the small coastal town ?
“Mỗi mùa hè, thị trấn nhỏ ven biển lại tổ chức màn bắn pháo hoa ngoạn mục.”
=> Every summer, the small coastal town puts up a breathtaking firework display.
“Bất chấp những lời đề nghị hấp dẫn, cô ấy vẫn tuân thủ kế hoạch ăn kiêng và tránh ăn những món ăn nhẹ không tốt cho sức?
“Bất chấp những lời đề nghị hấp dẫn, cô ấy vẫn tuân thủ kế hoạch ăn kiêng và tránh ăn những món ăn nhẹ không tốt cho sức khỏe.”
=> Despite the tempting offers, she sticks to her diet plan and avoids eating unhealthy snacks.
“Kinh nghiệm và trình độ chuyên môn của ứng viên cần đáp ứng được những yêu cầu của công ty.”
=> The candidate's exp?
“Kinh nghiệm và trình độ chuyên môn của ứng viên cần đáp ứng được những yêu cầu của công ty.”
=> The candidate's experience and qualifications need to meet the requirements of the company.
“Cơn mưa bão bất ngờ khiến cho nhiều người tham dự buổi sự kiện ngoài trời đến muộn.”
=> The unexpected rainstorm ca?
“Cơn mưa bão bất ngờ khiến cho nhiều người tham dự buổi sự kiện ngoài trời đến muộn.”
=> The unexpected rainstorm caused many attendees to turn on late for the outdoor event.
“Anh ấy rất giỏi giải quyết với những phàn nàn của khách hàng.”
=> He is good at handling with the complaints of cus?
“Anh ấy rất giỏi giải quyết với những phàn nàn của khách hàng.”
=> He is good at handling with the complaints of customers.
Mẫu sau ghi chép điểm số (thang điểm $100$ ) của $12$ thí sinh một trường THPT: ${\begin{array}{llllllllllll}58 & 74 & 9?
Mẫu sau ghi chép điểm số (thang điểm $100$ ) của $12$ thí sinh một trường THPT: ${\begin{array}{llllllllllll}58 & 74 & 92 & 81 & 97 & 88 & 75 & 69 & 87 & 69 & 75 & 77 .\end{array}}$
Khi đó:
“Phát hiện hàng bị hư hỏng, người mua ngay lập tức liên hệ người bán để yêu cầu hoàn lại toàn bộ số tiền.”
=> Discov?
“Phát hiện hàng bị hư hỏng, người mua ngay lập tức liên hệ người bán để yêu cầu hoàn lại toàn bộ số tiền.”
=> Discovering the item was damaged, the buyer promptly contacted the seller to request a full money return.
“Công ty quyết định giảm giá cho khách hàng trong lần mua tiếp theo.”
=> The company decided to offer customers a di?
“Công ty quyết định giảm giá cho khách hàng trong lần mua tiếp theo.”
=> The company decided to offer customers a discount on their next purchase.
“Chị gái tôi phàn nàn với quản lý về chất lượng dịch vụ kém mà chúng tôi nhận được ở nhà hàng.”
=> My sister made a ?
“Chị gái tôi phàn nàn với quản lý về chất lượng dịch vụ kém mà chúng tôi nhận được ở nhà hàng.”
=> My sister made a complaination to the manager about the poor service quality we received at the restaurant.
“Nhóm tiếp thị đã tiến hành nghiên cứu sâu rộng để xác định và hiểu được nhóm khách hàng tiềm năng.”
=> The marketin?
“Nhóm tiếp thị đã tiến hành nghiên cứu sâu rộng để xác định và hiểu được nhóm khách hàng tiềm năng.”
=> The marketing team conducted extensive research to identify and understand our target audience.
Kim loại nào sau đây khử được ion Zn2+?
Kim loại nào sau đây khử được ion Zn2+?
Thủy phân hoàn toàn tetrapeptit Ala-Gly-Ala-Val bằng enzim, thu được bao nhiêu loại amino axit?
Thủy phân hoàn toàn tetrapeptit Ala-Gly-Ala-Val bằng enzim, thu được bao nhiêu loại amino axit?
Chất nào sau đây thuộc loại polisaccarit?
Chất nào sau đây thuộc loại polisaccarit?
Không thể điều chế kim loại nào sau đây bằng phương pháp thủy luyện?
Không thể điều chế kim loại nào sau đây bằng phương pháp thủy luyện?
Polime có cấu trúc mạng lưới không gian là
Polime có cấu trúc mạng lưới không gian là
Kim loại X là kim loại cứng nhất, được sử dụng để mạ các dụng cụ kim loại, chế tạo các loại thép chống gỉ, không gỉ…Kim ?
Kim loại X là kim loại cứng nhất, được sử dụng để mạ các dụng cụ kim loại, chế tạo các loại thép chống gỉ, không gỉ…Kim loại X là?
Dung dịch muối nào sau đây bị phân hủy khi đun nóng?
Dung dịch muối nào sau đây bị phân hủy khi đun nóng?
Vật liệu tổng hợp X có dạng sợi dài, mảnh và giữ nhiệt tốt, thường dùng để dệt vải may quần áo ấm hoặc dệt thành sợi (le?
Vật liệu tổng hợp X có dạng sợi dài, mảnh và giữ nhiệt tốt, thường dùng để dệt vải may quần áo ấm hoặc dệt thành sợi (len) đan áo rét. X bền với nhiệt, bền trong môi trường axit và bazơ.Vật liệu X là
Loại dầu, mỡ nào dưới đây không chứa chất béo?
Loại dầu, mỡ nào dưới đây không chứa chất béo?
Phân tử etylamin có bao nhiêu nguyên tử hiđro?
Phân tử etylamin có bao nhiêu nguyên tử hiđro?
Dung dịch axit H2SO4 đặc, nguội phản ứng được với kim loại nào sau đây?
Dung dịch axit H2SO4 đặc, nguội phản ứng được với kim loại nào sau đây?
Chất nào sau đây có khả năng làm mềm nước cứng vĩnh cửu?
Chất nào sau đây có khả năng làm mềm nước cứng vĩnh cửu?
Ở điều kiện thường, chất nào sau đây tồn tại ở thể rắn, có cấu tạo ion lưỡng cực?
Ở điều kiện thường, chất nào sau đây tồn tại ở thể rắn, có cấu tạo ion lưỡng cực?
Dung dịch nào sau đây có pH < 7?
Dung dịch nào sau đây có pH < 7?
“Chiến dịch tiếp thị mới dự kiến sẽ thúc đẩy doanh số bán hàng đáng kể.”
=> The new marketing campaign is expected t?
“Chiến dịch tiếp thị mới dự kiến sẽ thúc đẩy doanh số bán hàng đáng kể.”
=> The new marketing campaign is expected to ____ sales significantly.
Dung dịch nào sau đây làm phenolphtalein đổi màu?
Dung dịch nào sau đây làm phenolphtalein đổi màu?
“Tôi mong muốn tham dự hội thảo tuần tới và học hỏi từ các chuyên gia trong ngành.”
=> I attending the conference n?
“Tôi mong muốn tham dự hội thảo tuần tới và học hỏi từ các chuyên gia trong ngành.”
=> I _____ attending the conference next week and learning from the industry experts.
“Trong tháng vừa qua, mức độ hài lòng của khách hàng đã giảm nhẹ.”
=> In the past month, there has been a in custom?
“Trong tháng vừa qua, mức độ hài lòng của khách hàng đã giảm nhẹ.”
=> In the past month, there has been a ____ in customer satisfaction ratings.
“Lời giải thích của cô ấy về chính sách mới rất khó hiểu đối với tôi.”
=> Her explanation of the new policy didn't ?
“Lời giải thích của cô ấy về chính sách mới rất khó hiểu đối với tôi.”
=> Her explanation of the new policy didn't ____ to me.
“Đặt mục tiêu rõ ràng là nền tảng để đạt được thành công trong bất cứ lĩnh vực nào của cuộc sống.”
=> clear goals i?
“Đặt mục tiêu rõ ràng là nền tảng để đạt được thành công trong bất cứ lĩnh vực nào của cuộc sống.”
=> ____ clear goals is the foundation for achieving success in any area of life.
“Mẹ tôi không thể tham dự buổi triển lãm nghệ thuật vì cô ấy phải làm thêm giờ tối nay.”
=> My mother can’t attend t?
“Mẹ tôi không thể tham dự buổi triển lãm nghệ thuật vì cô ấy phải làm thêm giờ tối nay.”
=> My mother can’t attend the art exhibition because she must work ____ tonight.
“Nhân viên mới bị sa thải vì đã tiết lộ tài liệu mật của công ty.”
=> “The new employee has because of leaking the ?
“Nhân viên mới bị sa thải vì đã tiết lộ tài liệu mật của công ty.”
=> “The new employee has ___ because of leaking the confidential document of the company.”
“Gia đình anh ấy luôn được ưu tiên hơn bạn bè và công việc của anh ấy.”
=> His family always his friends and work.
“Gia đình anh ấy luôn được ưu tiên hơn bạn bè và công việc của anh ấy.”
=> His family always ____ his friends and work.
“Khi nhìn thấy thiệt hại mà bão lũ đã gây ra cho nhà mình, cô ấy đã bật khóc.”
=> When she saw the damage the floods?
“Khi nhìn thấy thiệt hại mà bão lũ đã gây ra cho nhà mình, cô ấy đã bật khóc.”
=> When she saw the damage the floods had done to her house, she ______.
“Bất chấp áp lực to lớn, vận động viên cố gắng đáp ứng được kỳ vọng của người xem.”
=> Despite the immense pressure?
“Bất chấp áp lực to lớn, vận động viên cố gắng đáp ứng được kỳ vọng của người xem.”
=> Despite the immense pressure, the athlete manages to _____ the expectations of the spectators.
Cho mẫu số liệu thống kê về sản lượng chè thu được trong $1$ năm (kg/sào) của $10$ hộ gia đình:
Khi đó:
Cho mẫu số liệu thống kê về sản lượng chè thu được trong $1$ năm (kg/sào) của $10$ hộ gia đình:
Khi đó:
Thống kê số bao xi măng được bán ra tại một cửa hàng vật liệu xây dựng trong $24$ tháng cho kết quả như sau:
Khi đó:
Thống kê số bao xi măng được bán ra tại một cửa hàng vật liệu xây dựng trong $24$ tháng cho kết quả như sau:
Khi đó:
Số giờ học thêm ngoài trường học của $30$ học sinh được thống kê như sau:
Khi đó:
Số giờ học thêm ngoài trường học của $30$ học sinh được thống kê như sau:
Khi đó:
He returned from school. Then he got down to drinking water.
He returned from school. Then he got down to drinking water.
The concert started late. Many people left before it began.
The concert started late. Many people left before it began.
David has no sensation of responsibility because he never completes a task assigned to him.
David has no sensation of responsibility because he never completes a task assigned to him.
Her laptop crashed ten minutes ago and she still hasn't been able to turn them on.
Her laptop crashed ten minutes ago and she still hasn't been able to turn them on.
There is a sharp distinction between crimes which involves injury to people and those that don't.
There is a sharp distinction between crimes which involves injury to people and those that don't.
I hope my teacher will take into the fact that I was ill just before the exams when she marks my paper.
I hope my teacher will take into __________ the fact that I was ill just before the exams when she marks my paper.
The hospital is trying to raise for a new kidney machine.
The hospital is trying to raise __________ for a new kidney machine.
The old sports center by the authority and they are going to build a huge
shopping mall there.
The old sports center _________ by the authority and they are going to build a huge
shopping mall there.
The of responsibility to our department means a heavier workload.
The __________ of responsibility to our department means a heavier workload.
The government must now the problem of high unemployment.
The government must now ________ the problem of high unemployment.
One of their biggest priorities is to prevent costs from out of control.
One of their biggest priorities is to prevent costs from __________ out of control.
Huong is student in her class.
Huong is ______ student in her class.
She drove the wrong way down one-way street.
She drove the wrong way down __________ one-way street.
Thống kê chiều cao (đơn vị cm) của nhóm $15$ bạn nam lớp $10$ cho kết quả như sau:
Khi đó:
Thống kê chiều cao (đơn vị cm) của nhóm $15$ bạn nam lớp $10$ cho kết quả như sau:
Khi đó:
a commercial boost sponsor from the Empress Eugenie of France, the production manager is happy as a clam at high tide.
__________ a commercial boost sponsor from the Empress Eugenie of France, the production manager is happy as a clam at high tide.
A
______________________
Vietnam kicked much more convincingly in a 0-1 defeat when they reunited with Saudi Arabia at My Dinh November 16.
Vietnam kicked much more convincingly in a 0-1 defeat when they reunited with Saudi Arabia at My Dinh __________ November 16.
Social workers who look after abused or children often have stressful days at work.
Social workers who look after abused or __________children often have stressful days at work.
You may have dessert your lunch.
You may have dessert __________ your lunch.
Before I had dinner last night, the manager and accountant me to check the mail immediately.
Before I had dinner last night, the manager and accountant __________ me to check the mail immediately.
Jenny refused out for dinner with us yesterday because she had to complete
her assignment.
Jenny refused _________ out for dinner with us yesterday because she had to complete
her assignment.
His reaction is completely understandable, ?
His reaction is completely understandable, __________?
Tập đoàn ${X}$ có $24$ công ty. Thống kê cuối năm cho biết doanh thu (đơn vị triệu đồng) của $24$ công ty con như sau:
K?
Tập đoàn ${X}$ có $24$ công ty. Thống kê cuối năm cho biết doanh thu (đơn vị triệu đồng) của $24$ công ty con như sau:
Khi đó:
A
______________________
A
______________________
A
______________________
A
______________________
A
______________________
Cho các số phức $z,w$ thỏa mãn $\left| z \right|(2 + i) = \frac{{4z}}{w} + 3 - 4i$ và $\left| {{z^2} - 3 + 4i} \right| =?
Cho các số phức $z,w$ thỏa mãn $\left| z \right|(2 + i) = \frac{{4z}}{w} + 3 - 4i$ và $\left| {{z^2} - 3 + 4i} \right| = 9.$ Tích giá trị lớn nhất và nhỏ nhất của $\left| {w + 1 + 2i} \right|$ gần nhất với?
A
______________________
Cho hai đường $f(x) = \frac{{mx + n}}{{x + 1}}$ và $g(x) = a{x^2} + bx + c$ (với $a,b,c,m,n$ là các số thực) cắt nhau tạ?
Cho hai đường $f(x) = \frac{{mx + n}}{{x + 1}}$ và $g(x) = a{x^2} + bx + c$ (với $a,b,c,m,n$ là các số thực) cắt nhau tại ba điểm phân biệt có hoành độ $ - 2;1;2.$ Hàm số $h(x) = (x + 1)g(x) - (m + 9)x - n$ có giá trị cực đại bằng $ - 9.$ Diện tích hình phẳng giới hạn bởi các đường $y = f(x);y = g(x)$ và hai đường thẳng $x = 0;x = 1$ bằng
Trong không gian với hệ tọa độ $Oxyz$, cho hình lăng trụ đứng $ABC.A'B'C'$ có $A\left( {{x0};0;0} \right)$ $B\left( { - ?
Trong không gian với hệ tọa độ $Oxyz$, cho hình lăng trụ đứng $ABC.A'B'C'$ có $A\left( {{x_0};0;0} \right)$ $B\left( { - {x_0};0;0} \right)$, $C\left( {0;1;0} \right)$ và $B'\left( { - {x_0};0;{y_0}} \right)$ trong đó ${x_0};{y_0}$ là các số thực dương và thỏa mãn ${x_0} + {y_0} = 4.$ Khi khoảng cách giữa hai đường thẳng $AC'$ và $B'C$ lớn nhất thì bán kính $R$ của mặt cầu ngoại tiếp hình lăng trụ $ABC.A'B'C'$ bằng bao nhiêu?
Xét hai điểm $A,\,B$ lần lượt là các điểm trong mặt phẳng $Oxy$ biểu diễn các số phức $z$ và $\left( {1 + 3i} \right)z$ ?
Xét hai điểm $A,\,B$ lần lượt là các điểm trong mặt phẳng $Oxy$ biểu diễn các số phức $z$ và $\left( {1 + 3i} \right)z$
và diện tích của tam giác $OAB$ bằng 6. Gọi $w$ là số phức thỏa mãn $\left| {z - 2w} \right| = \left| {z + 2w} \right| = 4.$ Tính $\left| w \right|.$
Trong không gian $Oxyz,$ cho tam giác $ABC$ vuông tại $A,BC=3\sqrt{2},\overset\frown{ABC}={{30}^{\circ }}.$ Đường thẳng ?
Trong không gian $Oxyz,$ cho tam giác $ABC$ vuông tại $A,BC=3\sqrt{2},\overset\frown{ABC}={{30}^{\circ }}.$ Đường thẳng $BC:\frac{{x - 4}}{1} = \frac{{5 - y}}{{ - 1}} = \frac{{z + 7}}{{ - 4}}$, đường thẳng $AB$ nằm trong mặt phẳng $(P):x + z - 3 = 0$ và điểm $A(a;b;c).$ Tính $a + b + c$
Cho hàm số $f(x) = \frac{{\left[ {a\ln (x - 3) + x} \right]a + 1 - 4a}}{{{3^x}}}$ với $a$ là tham số thực. Gọi $T$ là tí?
Cho hàm số $f(x) = \frac{{\left[ {a\ln (x - 3) + x} \right]a + 1 - 4a}}{{{3^x}}}$ với $a$ là tham số thực. Gọi $T$ là tích các giá trị của $a$ để hàm số $f(x)$ có giá trị lớn nhất trên $\left( {3; + \infty } \right)$ không vượt quá $\frac{1}{{81}}.$ $T$ nằm trong khoảng nào sau đây?
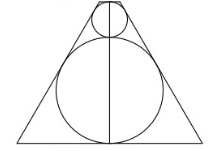
Người ta sản xuất một vật lưu niệm $(X)$ bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết diện qua trục là một ?
Người ta sản xuất một vật lưu niệm $(X)$ bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết diện qua trục là một hình thang cân. Bên trong $(X)$ có 2 khối cầu ngũ sắc với bán kính $R = 3,r = 1$ tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của $(X)$ đồng thời 2 khối cầu tiếp xúc với 2 đáy của $(X).$ Tính thể tích vật lưu niệm đó, làm tròn đến hàng đơn vị.
Cho hình lăng trụ $ABC.A'B'C'$ có tất cả các cạnh bằng $a.$ Gọi $M,N$ lần lượt là trung điểm của $AC,AC'.$ Biết $AN = \f?
Cho hình lăng trụ $ABC.A'B'C'$ có tất cả các cạnh bằng $a.$ Gọi $M,N$ lần lượt là trung điểm của $AC,AC'.$ Biết $AN = \frac{{a\sqrt 7 }}{2}$ và $BM \bot AN.$ Thể tích khối lăng trụ trên là?
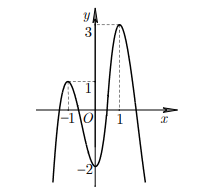
Cho hàm số $y = f(x)$ liên tục trên $R$ và có đồ thị như hình vẽ. Tính $\int\limits{1 - \sqrt 2 }^1 {(x - 1)\left| {f'({?
Cho hàm số $y = f(x)$ liên tục trên $R$ và có đồ thị như hình vẽ. Tính $\int\limits_{1 - \sqrt 2 }^1 {(x - 1)\left| {f'({x^2} - 2x)} \right|} dx$
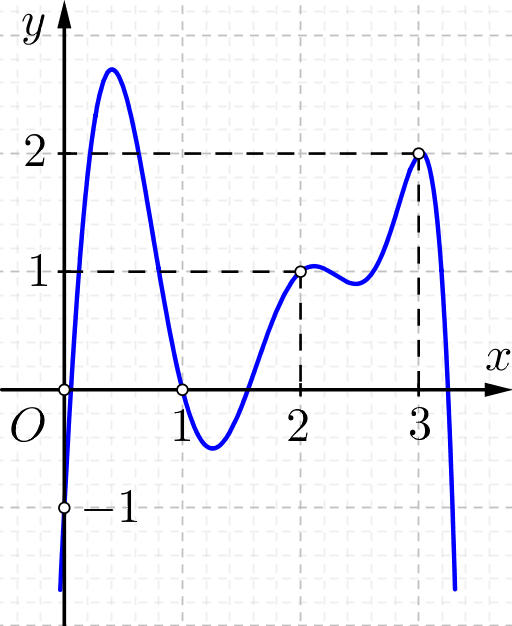
Cho hàm số $f(x)$ có bảng biến thiên như sau. Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y = \frac{{{?
Cho hàm số $f(x)$ có bảng biến thiên như sau. Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y = \frac{{{{\log }_2}(6x - m)}}{{{f^2}(x) - 2f(x)}}$ có tổng cộng 4 đường tiệm cận đứng và ngang?
Cho hàm số $f(x) = \left| {\frac{{m{x^2} - x + m}}{{{x^2} + 1}}} \right|$ có tối đa bao nhiêu điểm cực trị?
Cho hàm số $f(x) = \left| {\frac{{m{x^2} - x + m}}{{{x^2} + 1}}} \right|$ có tối đa bao nhiêu điểm cực trị?
Tỉnh Nam Định đưa ra quyết định về việc giảm biên chế nhà nước trong giai đoạn 5 năm từ $2025 - 2030$ với mục tiêu là 12?
Tỉnh Nam Định đưa ra quyết định về việc giảm biên chế nhà nước trong giai đoạn 5 năm từ $2025 - 2030$ với mục tiêu là 12% so với số lượng ban đầu. Giả sử tỉ lệ giảm biên chế hằng năm là như nhau. Để đạt được mục tiêu đề ra, tỉnh Nam Định cần phải thực hiện giảm mỗi năm tối thiểu bao nhiêu phần trăm?
Có bao nhiêu số phức $z$ thỏa mãn $\left| {z + 2 - i} \right| = 2\sqrt 2 $ và ${\left( {z - i} \right)^2}$ là số thuần ả?
Có bao nhiêu số phức $z$ thỏa mãn $\left| {z + 2 - i} \right| = 2\sqrt 2 $ và ${\left( {z - i} \right)^2}$ là số thuần ảo?
Số đường tiệm cận đứng và ngang của đồ thị hàm số $y = \frac{{\log x}}{{x - 2}}$ là?
Số đường tiệm cận đứng và ngang của đồ thị hàm số $y = \frac{{\log x}}{{x - 2}}$ là?
Cho hai điểm $A\left( {3;\;3;\;1} \right)$, $B\left( {0;\;2;\;1} \right)$ và mặt phẳng $\left( P \right):x + y + z - 7 =?
Cho hai điểm $A\left( {3;\;3;\;1} \right)$, $B\left( {0;\;2;\;1} \right)$ và mặt phẳng $\left( P \right):x + y + z - 7 = 0.$ Gọi $d$ là đường thẳng nằm trên $\left( P \right)$ sao cho mọi điểm của $d$ cách đều hai điểm $A$ và $B.$ Phương trình của đường thẳng $d$ là:
A
______________________
Cho hình chóp tam giác đều $S.ABC$ cạnh đáy bằng $2a$ và chiều cao bằng $a\sqrt 3.$ Tính khoảng cách từ tâm $O$ của đáy ?
Cho hình chóp tam giác đều $S.ABC$ cạnh đáy bằng $2a$ và chiều cao bằng $a\sqrt 3.$ Tính khoảng cách từ tâm $O$ của đáy $ABC$ đến một mặt bên.
A
______________________
Trong một hộp có $30$ viên bi đánh số từ $1$ đến $30$, lấy ngẫu nhiên ra hai bi. Tính xác suất để hai bi lấy ra có tích ?
Trong một hộp có $30$ viên bi đánh số từ $1$ đến $30$, lấy ngẫu nhiên ra hai bi. Tính xác suất để hai bi lấy ra có tích hai số trên chúng là một số chia hết cho 3.
Cho số phức $z = 1 + 3i$, môđun của số phức $w = {z^2} - i\overline z $ là
Cho số phức $z = 1 + 3i$, môđun của số phức $w = {z^2} - i\overline z $ là
Trong các hàm số sau, hàm số nào đồng biến trên $\mathbb{R}$?
Trong các hàm số sau, hàm số nào đồng biến trên $\mathbb{R}$?
Cho số phức $z = - 1 + 2i.$ Số phức $\overline z $ được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ?
Cho số phức $z = - 1 + 2i.$ Số phức $\overline z $ được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ?
Tìm tập nghiệm của bất phương trình ${\left( {\frac{1}{2}} \right)^{{x^2} - x}} > {\left( {\frac{1}{2}} \right)^{4 - x}}?
Tìm tập nghiệm của bất phương trình ${\left( {\frac{1}{2}} \right)^{{x^2} - x}} > {\left( {\frac{1}{2}} \right)^{4 - x}}.$
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {1;2; - 3} \right)$, $B\left( { - 2;3;1} \right)$ đường thẳ?
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {1;2; - 3} \right)$, $B\left( { - 2;3;1} \right)$ đường thẳng đi qua $A\left( {1;2; - 3} \right)$ và song song với đường thẳng $OB$ có phương trình là:
Đường tiệm cận ngang của đồ thị hàm số $y = \frac{{x + 1}}{{x - 2}}$ là đường thẳng:
Đường tiệm cận ngang của đồ thị hàm số $y = \frac{{x + 1}}{{x - 2}}$ là đường thẳng:
Tích phân $\int\limits1^2 {{{\left( {x + 3} \right)}^2}{\rm{d}}x} $ bằng:
Tích phân $\int\limits_1^2 {{{\left( {x + 3} \right)}^2}{\rm{d}}x} $ bằng:
Trong không gian $Oxyz$, mặt phẳng chứa hai điểm $A\left( {1;\;0;\;1} \right)$, $B\left( { - 1;\;2;\;2} \right)$ và song?
Trong không gian $Oxyz$, mặt phẳng chứa hai điểm $A\left( {1;\;0;\;1} \right)$, $B\left( { - 1;\;2;\;2} \right)$ và song song với trục $Ox$ có phương trình là:
Trong không gian $Oxyz$, cho hai điểm $A\left( {2;\;3;\;5} \right)$ và $B\left( {4;\; - 5;\;7} \right).$ Phương trình mặ?
Trong không gian $Oxyz$, cho hai điểm $A\left( {2;\;3;\;5} \right)$ và $B\left( {4;\; - 5;\;7} \right).$ Phương trình mặt cầu đường kính $AB$ là:
Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right) = \frac{{2x - 1}}{{x + 1}}$ ?
Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right) = \frac{{2x - 1}}{{x + 1}}$ trên đoạn $\left[ {0;3} \right].$ Tính giá trị $M - m.$
Tích các nghiệm của phương trình $\log {(x - 1)^2} = 2$ là:
Tích các nghiệm của phương trình $\log {(x - 1)^2} = 2$ là:
Cho $a$ là số dương, biểu thức ${a^{\frac{2}{3}}}.\sqrt a $ viết dưới dạng lũy thừa với số mũ hữu tỉ là:
Cho $a$ là số dương, biểu thức ${a^{\frac{2}{3}}}.\sqrt a $ viết dưới dạng lũy thừa với số mũ hữu tỉ là:
Cho tứ diện $OABC$ có $OA$, $OB$, $OC$ đôi một vuông góc với nhau tại $O$ và $OA = 2$, $OB = 4$, $OC = 6.$ Thể tích khối?
Cho tứ diện $OABC$ có $OA$, $OB$, $OC$ đôi một vuông góc với nhau tại $O$ và $OA = 2$, $OB = 4$, $OC = 6.$ Thể tích khối tứ diện $OABC$ bằng
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và bảng xét dấu của đạo hàm như sau: AHỏi hàm số $y = f\?
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và bảng xét dấu của đạo hàm như sau:
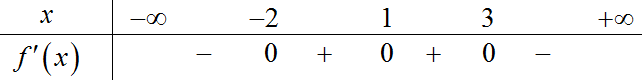
Hỏi hàm số $y = f\left( x \right)$ có bao nhiêu điểm cực trị?
Trong không gian $O & xyz\,,$cho đường thẳng $d:\frac{{x + 8}}{4} = \frac{{y - 5}}{{ - 2}} = \frac{z}{1}\,.$ Khi đó vect?
Trong không gian $Oxyz$, cho đường thẳng $d:\frac{{x + 8}}{4} = \frac{{y - 5}}{{ - 2}} = \frac{z}{1}\,.$ Khi đó vectơ chỉ phương của đường thẳng $d$ có tọa độ là:
Cho hình nón $\left( N \right)$ có đường kính đáy bằng $4a$, đường sinh bằng $5a.$ Tính diện tích xung quanh $S$ của hìn?
Cho hình nón $\left( N \right)$ có đường kính đáy bằng $4a$, đường sinh bằng $5a.$ Tính diện tích xung quanh $S$ của hình nón $\left( N \right).$
Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{\left( {x - 5} \right)^2} + {\left( {y + 1} \right)^2} + {\left(?
Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{\left( {x - 5} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 16.$ Tâm I của mặt cầu$\left( S \right)$ có tọa độ là:
Cho hàm số $y = f\left( x \right)$, có bảng biến thiên như sau: AMệnh đề nào dưới đây đúng?
Cho hàm số $y = f\left( x \right)$, có bảng biến thiên như sau:
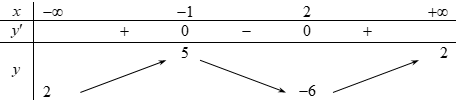
Mệnh đề nào dưới đây đúng?
Cho cấp số nhân $\left( {{un}} \right)$ có số hạng đầu ${u1} = 5$ và công bội $q = - 2.$ Giá trị của ${u6}$ bằng:
Cho cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = 5$ và công bội $q = - 2.$ Giá trị của ${u_6}$ bằng:
Cho $\int\limits{ - 2}^1 {f\left( x \right)\,{\rm{d}}x} = 3.$ Tính tích phân $I = \int\limits{ - 2}^1 {\left[ {2f\left(?
Cho $\int\limits_{ - 2}^1 {f\left( x \right)\,{\rm{d}}x} = 3.$ Tính tích phân $I = \int\limits_{ - 2}^1 {\left[ {2f\left( x \right) - 1} \right]{\rm{d}}x}.$
Cho hàm số $f\left( x \right) = {x^2} - 3x + \frac{1}{x}.$ Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số $f\left( x \right) = {x^2} - 3x + \frac{1}{x}.$ Trong các khẳng định sau, khẳng định nào đúng?
_______________________
Cho số phức ${z1} = 1 + 2i$ và ${z2} = - 2 - 2i.$ Tìm môđun của số phức ${z1} - {z2}.$
Cho số phức ${z_1} = 1 + 2i$ và ${z_2} = - 2 - 2i.$ Tìm môđun của số phức ${z_1} - {z_2}.$